Interactive Lecture Demonstration 19

Interactive Lecture Demonstration 17 – Mass on Spring

In this demonstration, a mass hangs from a spring. When the mass is pulled away from its equilibrium position and released, it will oscillate up and down in simple harmonic motion, because the net force on the mass is proportional to (and opposite to) the displacement from equilibrium. We will investigate the position, velocity, acceleration and force as a function of time for the oscillating mass, and compare the maximum values of these quantities to those calculated using the measured amplitude and period of the motion. We will use a sonic ranger to determine the position, velocity and acceleration of the mass, and a force sensor to measure the force of the spring on the mass.

In this activity and in the Followup homework problems, we will use the following physics laws:

Hooke's Law for an ideal spring: F_spring = - k x, where x is the position of the end of the spring relative to its unstretched position; k is called the spring constant and describes how hard it is to stretch the spring. In any situation (even when we are not dealing with a spring) when the force on an object is directed towards an equilibrium position and is directly proportional to the displacement of an object from equilibrium, we will say that the force on the object obeys Hooke's Law.

If the net force on any object obeys Hooke's Law, that object will always move in simple harmonic motion (SHM). SHM is defined to be motion where the equation of position versus time for the object is: x(t) = A cos(wt) + x_eqwhere A is the amplitude of the motion, w is the angular frequency (related to the frequency by w = 2pf and to the period by w = 2p/P) and x_eqis the equilibrium position. This equation assumes that at t = 0, x = A + x_eq, i.e. the object is at its maximum displacement from equilibrium.

For any object moving in simple harmonic motion, the angular frequency is related to the ratio of two properties of the system: the restoring force that tends to bring the object back to its equilibrium position, and the inertia of the object. For a mass on a spring, this relationship is:

w = √ k/m (for other systems, for example a pendulum, we will have a similar looking equation).

Any system that obeys Hooke's Law possesses a potential energy that is given by: PE = (1/2) k x². This represents the energy stored in the system when it has been stretched (or compressed) from its unstretched position by an amount x.

We will consider all of these to be basic laws of physics. Any other formulas or results that we want to use (for example, some of the other formulas given in the textbook for objects moving in simple harmonic motion) will have to be derived from these.

1. A mass m is hung from a vertical spring of spring constant k. When the mass is stationary, the spring is stretched an amount, x_eq from its unstretched position. Create the appropriate force diagram and do the net force problem to find an expression relating x_eq to m, g, and k. This requires 2 pictures, one showing the unstretched spring, one showing the stretched one. See the leftmost 2 pictures below.

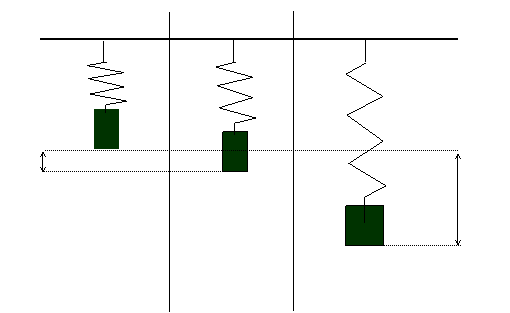
2. We will set the spring into oscillation by lifting it up (but not so much as to completely relax the spring) and releasing it. Use a watch or the clock on the classroom wall to measure the period of oscillation. To get an accurate measurement, time at least 10 oscillations and find the average period.

3. The mass hanging from the spring is about 620 grams. The spring constant is about 12 N/m. Use this data to predict the period of the motion. Compare your calculation with the period you measured. The formula for the period assumes that the spring is much less massive than the hanging mass; our spring is only about 4 or 5 times lighter than the hanging mass, so our predicted value here will probably be somewhat different than the measured value.

6. Read the x and t coordinates of three consecutive extremum points. (An extremum point is a peak or a valley.) These points span one complete cycle of the motion. Record the results with units. Use the data to calculate the period of the motion. Show your work. As a check, this value should be within 5% of the value you already measured.

7. Use the data you collected in the last step to calculate the equilibrium position. Show your work. Compare your calculated value with the equilibrium position you measured.

8. Use the step 6 data to calculate the amplitude of the motion. Show your work.

9. Determine the equation for the position, y, of the spring as a function of time, t, assuming that the mass was at its maximum position when t = 0. You’ll need to decide how the constants of the motion calculated in 6, 7 and 8 will be incorporated into the equation. Give the equation in symbols first, and then substitute constants with units.

10. Now examine the velocity vs time, acceleration vs time and force vs time graphs that correspond to the position vs time graph you just made. On the next page, sketch all four graphs. Put the velocity, acceleration and force graphs directly beneath the position graph, using the same time scale. Put scales and units on all your axes.

A) Where (in position) is the mass when the velocity is a maximum? What is this velocity? What is the acceleration at this point? Where, relative to its equilibrium position, is the mass at this point (at equilibrium, above equilibrium, below equilibrium ?)

B) Where is the mass when the acceleration is a maximum? What is the value of the maximum acceleration? What is the velocity at this point? Where, relative to its equilibrium position, is the mass at this point (at equilibrium, above equilibrium, below equilibrium ?)

C) Does the maximum acceleration magnitude occur at the same time as the maximum force magnitude? What physics predicts that it should? (remember what force is being graphed !)

D) Does the maximum displacement magnitude occur at the same time as the maximum acceleration magnitude? What physics predicts that it should?

One way to summarize some of the results above is to say that the position and velocity are 90° (1/4 cycle) out of phase, and position and acceleration are 180° (1/2 cycle) out of phase. Net force and acceleration, though are 0° out of phase – that is, they are in phase.